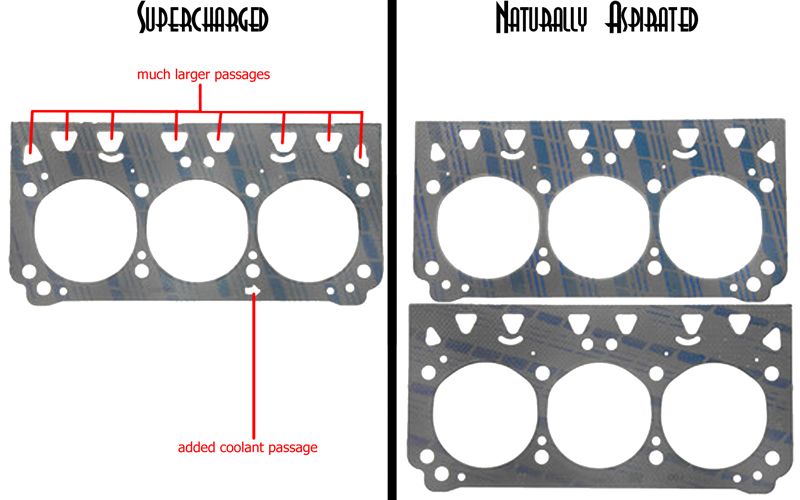
In my experience dealing with online vendor's there's seems to be no rhyme or reason for the prices that some charge compared to others. If dimensionally the gaskets look the same one on top of the other then I'd just get a cheap pair.
Their gaskets, cheap or pricey their only purpose is to create a seal. As long as thats acheived you should be good. I couldn't see why the 3800SC would use different gaskets, perhaps the S/C ones are made of a different material because of the higher compression but I'm not 100% sure.
I would only suggest spending more $$$ on higher quality gaskets if your running headers. A buddy of mine has a 385 Stroker in his 88' GTA and the header bolts over time like to loosen a bit, his gaskets seal while also holding his bolts more snuggly because of slightly undersized bolt holes.
Good luck in your search!